Options in Fixed Income Part 2: No, Debt is TWO Puts!

Examining debt's sensitivity to volatility and value from an options trading lens.

Hey everyone, today we are continuing with the theme of the last piece linked here. Please reach out if you have feedback or would like to discuss the ideas further (ejn2@williams.edu).

Introduction

Last week, I provided an introduction to the basics of options and options pricing. I then expanded this view to talk about how equity is a quasi-call option on the enterprise value of a company struck at the debt burden. I further mentioned debt could be viewed as selling a quasi put option. Probably more accurately, buying corporate debt is akin to being long a risk-free bond and short a put option on the EV of the business. I will review these points in this piece.

Importantly, I will try to offer a more precise view of credit.¹ Buying debt is not as simple as being short a put option on the EV of a company. Instead, it is more similar to being short a put option on EV at a strike price of the total debt burden and long a second put option struck at all debt senior to it. This is rather complicated and I will try to simplify this throughout the paper. I will then write about the implications of this view on credit investing. Most interesting, the distressed creditor, rather than being short a put option, appears to have a quasi-call option on the company.

The purpose of this paper and the last one are to set up a counterintuitive framework for credit investing. I will then try to apply this framework to explore potential trade ideas in the next piece. The third part of this series will likely take a bit longer to complete, apologies in advance.

Roadmap

1. Last Week Review: Equity is a Call, Debt is Short a Put

2. Debt is Short a Put and Long a Put!

3. Delta of the Bond Holder

4. Vega of the Bond Holder

5. Conclusion

Equity is a Call, Debt is Short a Put

Equity = Call on EV

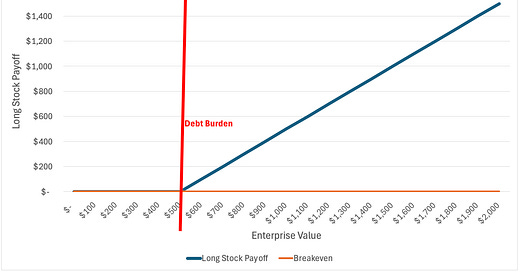
It’s worth reviewing the end of last week’s piece where I talked about equity and debt as very similar to options. Owning stock has practically identical payoffs to owning a call option struck at the value of debt. Equity receives all the upside of the value of the company after debt is paid off. Stockholders' downside is limited to their equity investment, just like call owners (Figure 1).

Figure 1: Being Long a Company’s Stock has Payoffs Similar to Long a Call Option on EV

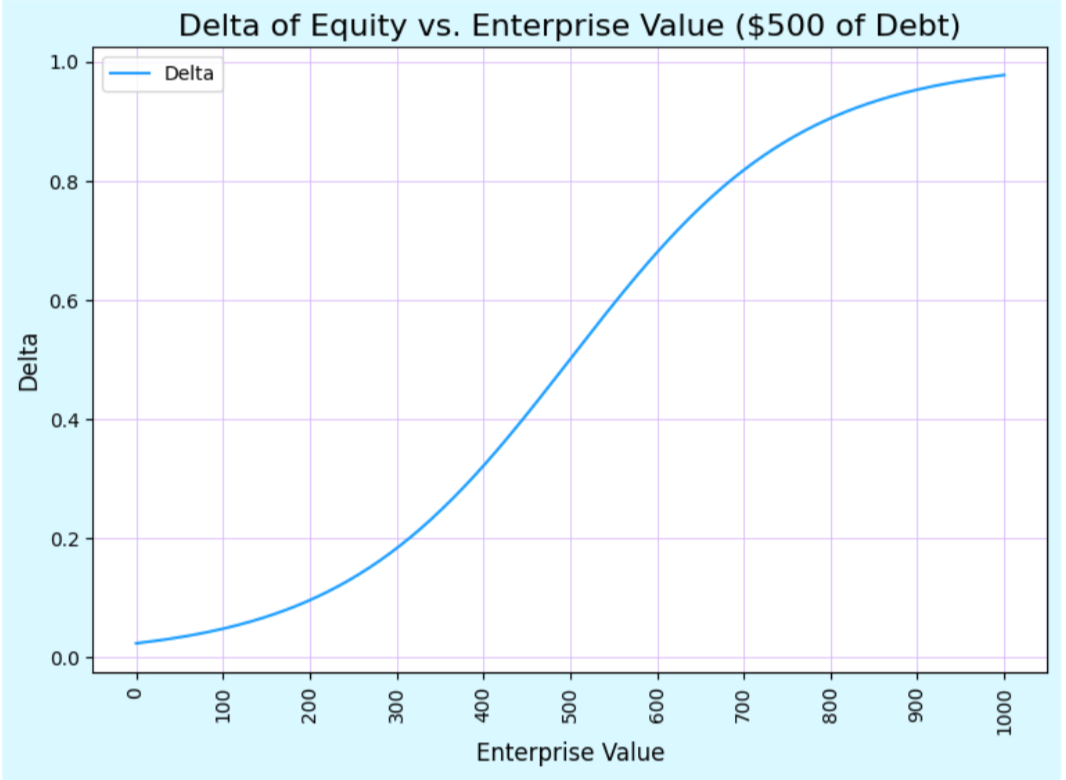
The greater the intrinsic value of the equity (more solvent the company/right hand side of the diagram), the more directly the change in underlying asset value is reflected in the change in stock price. This is called the delta of the stock with respect to the EV. This is hard to see in the payoff diagram as the payoff diagram only focuses on the payoff at expiration. As a rule, deltas are ~.50 for ATM calls and increase as the call becomes more ITM. Below is a hypothetical illustration of how much the stock might move for a given change in EV. When the stock is ATM (company is barely solvent), a $1 increase in EV should equate to a ~$.50 increase in equity value. When the stock is very ITM (EV = $1,000), a $1 increase in EV should equate to almost a $1 increase in equity value (Figure 2).

Figure 2: Hypothetical Illustration of the Delta of the Stock wrt EV

Let’s now briefly look at the vega of the stockholder. As a reminder, vega is the sensitivity (derivative) of equity value with respect to changes in volatility of the enterprise value. Last week, I mentioned equity owners are long vega, or benefit from volatility/uncertainty in the assets of the company. The chart below is for illustrative purposes only and not for a specific situation. As you can see, the stock benefits more from increases in volatility the lower the intrinsic value of the stock (up to a point). Vega is highest for ATM options. That is, the closer the stock is to insolvency (debt burden point), the more the stock owner wants volatility. Stocks are almost always long vol, they are just significantly more so when the company is closer to insolvency (Figure 3).

Figure 3: Hypothetical Illustration of the Vega of the Stock wrt EV

Debt = Short a Put on EV?

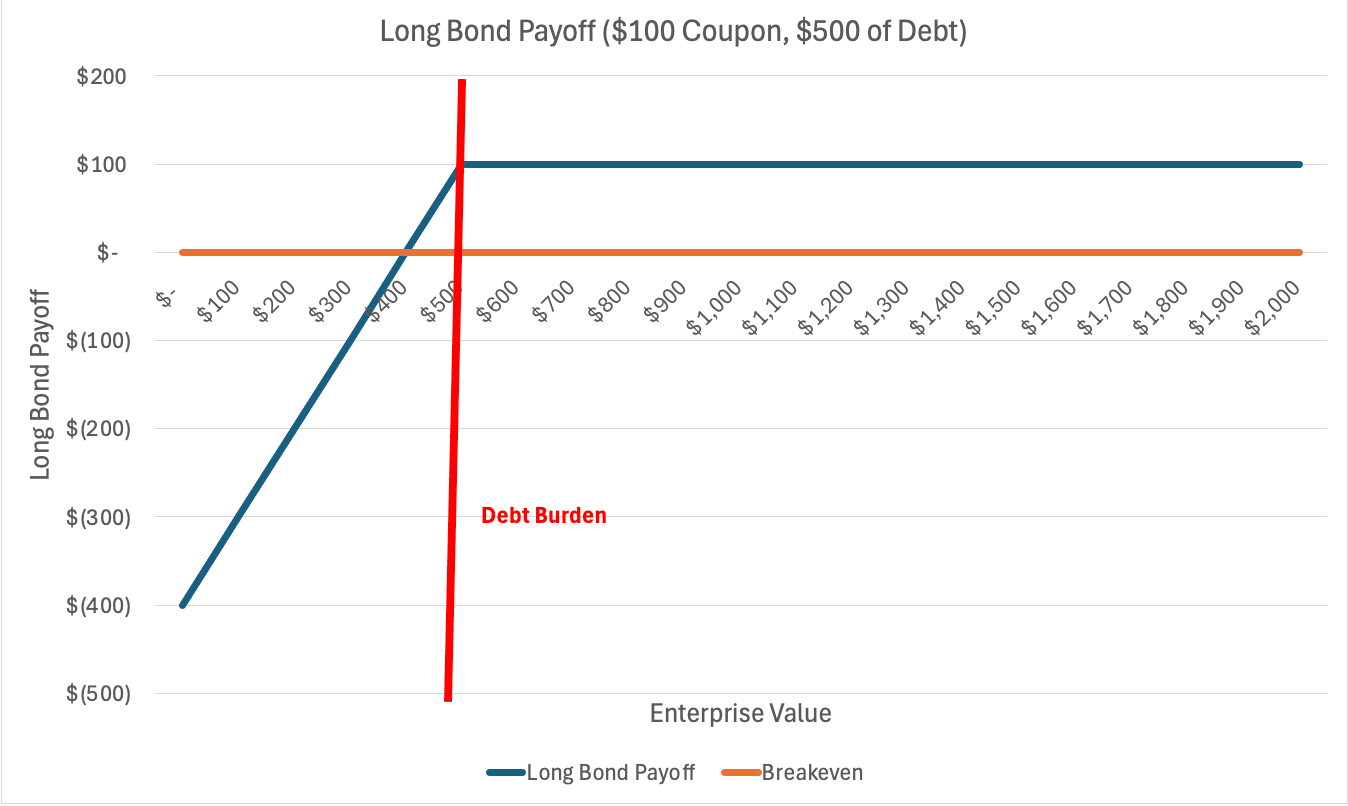
Before I add a corollary to this, let’s review the statement from last week that debt is akin to selling a put option on EV. The long bond position has a similar payoff to the put seller at a strike price of debt. As soon as EV falls below $500, the put seller (bond holder) begins to take some loss (ignoring coupon payments). When EV is above the debt burden, the bondholder receives the full principal payment (Figure 4). This implies the bondholder is long delta and short vega—the bondholder wants the stock to rise and wants volatility to fall. However, as we will see later, this is not always the case!

Figure 4: Long Bond Position is Similar to Selling a Put on EV

No, Debt is Actually Short a Put Spread!

Yet, credit is not so simple. Unsecured credit is more akin to being short a put on the assets of the company and long a put with a strike of all debt senior to it. This is a bit complicated, so let’s look at the balance sheet below (Figure 5).

Figure 5: Hypothetical Balance Sheet of Company ABC

The owner of the unsecured bonds (Jr. Debt) is short a put option at $80 of EV and long a second put option at $10 of EV. Let’s first go through the situational payoffs for the junior debt and then illustrate the payoff diagram.

1. If Company ABC has assets >= $80→ the debt investor suffers no losses. Principle and coupon is paid, akin to selling a put option that expires OTM.

2. If Company ABC has assets between $10 and $80 → the investor suffers losses equal to $80 - Asset Value (ignoring coupon payments). So, if assets are $50, the investor suffers $30 of losses.

   1. The $50 of assets first go to pay down $10 of senior debt. There is then $40 left over and $70 of junior debt, leaving the junior debt with $30 in losses.

3. If Company ABC has assets less than $10 → The investor suffers $70 of losses. The losses are effectively capped at $70 as the senior debt takes losses past this point.

   1. If the company has $0 in assets, junior debt only loses $70 and senior debt takes the additional $10 hit.

   2. This is similar to selling a put spread (selling a high strike put and buying a low strike put) on the EV of the company.

Below, I’ve illustrated the payoff from the long unsecured bond position (Figure 6). For simplicity, I’ve assumed the $10 coupon is always paid. Changing this assumption would just lead to a kink in the payoff diagram. I’ve also illustrated the payoff from the long put position struck at the level of senior debt (Figure 7) and the short put position struck at the level of unsecured debt (Figure 8). By summing up the two put positions, you can arrive at the long unsecured bond position—implying the bond is simply a put spread on EV.

Figure 6: Payoff Diagram of Buying the Unsecured Bonds of ABC

Figure 7: Payoff Diagram of Selling a $80 Strike Put on EV (+$10 Coupon Always)

Figure 8: Payoff Diagram from Buying the $10 Strike Put

Repeating this again:

1. When the EV is above the value of all debt outstanding, the payoff is the par value of the bond (+ coupon payments).

2. When the EV is above the value of the secured debt, but below that of all debt outstanding, the payoff is the same as if the short put is exercised by ITM. The payoff is the par value of the bond - net loss on the option.

3. When the EV is less than the value of secured debt, the payoff on the long option cancels out any further losses on the short put option and the payoff is 0 (defined as losing the par value of the bond + coupons), but not less than 0!

Delta of the Debt Holder

This now brings up interesting implications. In the last piece, when I simplified debt to simply selling a put option on the assets of the company the delta was easy to calculate. The delta was always positive and higher for lower asset values than higher asset values. Now, however, we have two puts—one short and one long. The delta of the total position is the sum of the individual deltas. Let’s imagine company ABC grows and now has the balance sheet shown in Figure 9.

Figure 9: Hypothetical Balance Sheet of Company ABC for the Remainder

First, some basic options theory. We’ve already touched on a lot of this, but repeating it should be helpful for those new to options. Deltas are often proxies for the probability an option expires ITM.

1. Options that are far OTM have deltas approaching 0 as small changes in underlying values for deep OTM options don’t affect the probability it pays off significantly. 

   1. There is basically no chance a $100 strike call option expires ITM for a stock trading at $5 today and thus a $1 move in the stock probably won’t change the price of the call that much.

2. Options that are ATM have deltas around +/-.50 (depending on call vs. put) as there is a 50% chance the stock winds up ITM and the $1 rise is directly reflected in intrinsic value and a 50% chance the stock winds up OTM and the $1 move has a $0 effect on intrinsic value.

   1. When the stock is at $100, the $100 strike call option has a ~.5 delta, meaning the stock rising $1 will lead to the call rising ~$.50.

3. Options that are deep ITM have deltas around +/- 1 (depending on call vs. put) as the stock is highly likely to wind up ITM and changes in the underlying closely translate to higher intrinsic value of the option.

   1. When the stock is at $1,000, the $100 strike call option has a ~1 delta as a $1 move in the underlying (from $1,000 to $1,001), leads the value of the call option up almost $1.

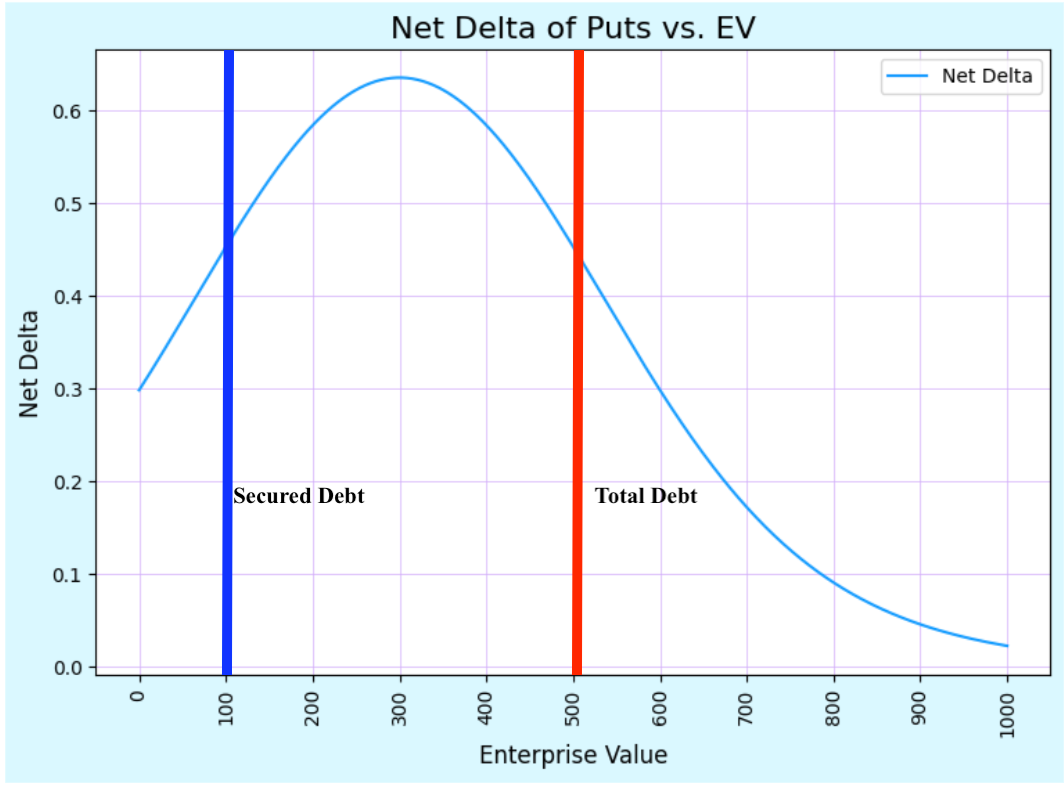
Ok, so the lower the EV, the more ITM both put options become. The sold put will always be more ITM than the bought put. The higher the EV, the more OTM both puts become. As the EV increases, the delta of both puts approaches 0. As the EV falls, the delta of the sold put approaches 1, while the delta of the bought put also approaches -1 but is always below the delta of the sold put (in absolute value). A graph of both puts is shown below (Figure 10). The long bond position has a net delta equal to the sum of both options. This graph is shown below as well (Figure 11). When the EV is between the strike of both puts, the delta is greatest. Thus, at around these points the bond position becomes most sensitive to changes in the underlying asset value. 

Figure 10: Delta of the Long $100 Strike Put and Short $500 Strike Put

Figure 11: Combined Delta of the Long Unsecured Bond Position (Sum of the Put Deltas)

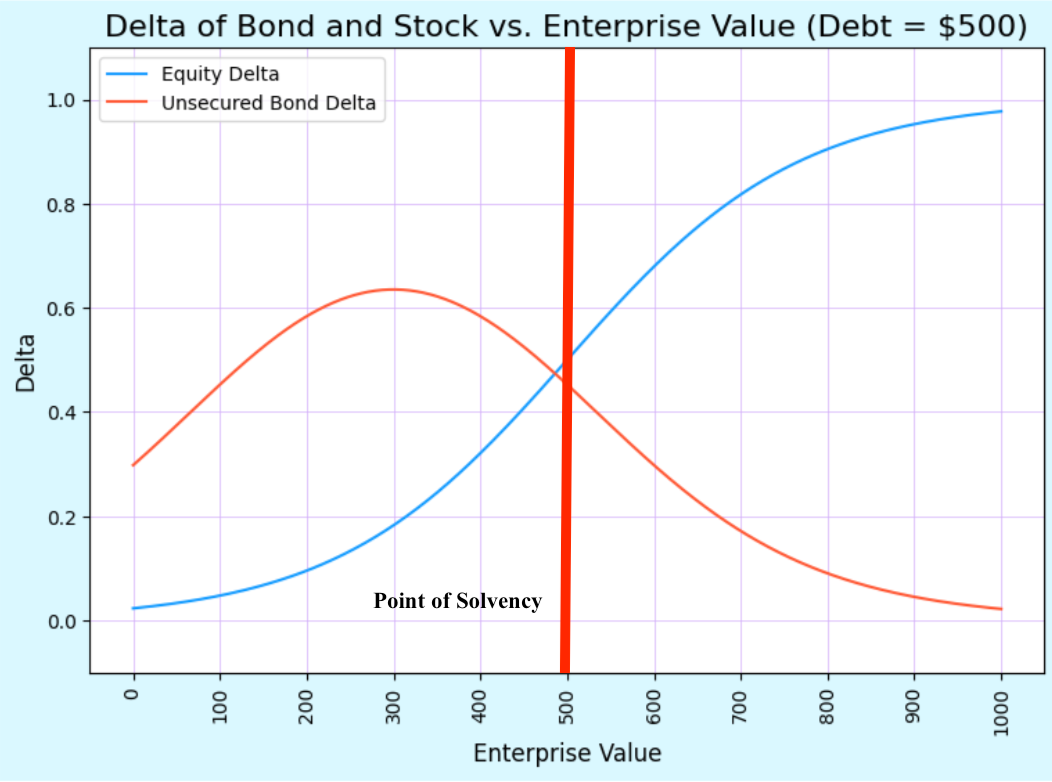
Between the strike of both puts the bond position has the highest delta. This is also where the unsecured bond is considered “distressed.” Thus, the bond becomes to have “equity-like” characteristics (high delta) when it becomes more distressed. Equity generally has high delta when the company is solvent. The chart below should illustrate why the distressed bond appears “equity-like” (Figure 12). When the company becomes insolvent, the delta of the bond position is actually above the delta of the equity position!

Figure 12: Delta of Equity vs. Stock wrt EV

Vega of the Bond Holder

Ok, so when a bond is distressed, the delta makes it act “equity-like.” But, bond holders must always hate volatility, right? Nope. In last week’s piece, when I simplified bonds as short put options, the bond was always short vega—its value decreased as implied volatility increased. However, we now have two options, one short and one long. The long option will always be positive vega while the short option will always be negative vega. The combined vega position of the bond is simply the sum of the two vegas. First, some basic vega theory. I am linking last week’s code sample so the reader can try out the vega assumptions (change implied volatility and see how the option price changes depending on whether the option is OTM, ITM, or ATM).

1. Vega is highest for ATM options

   1. ATM options prices are largely driven by the time/extrinsic value of the option. Changes in implied volatility directly affect the time value. 

2. Vega approaches 0 as the option becomes highly ITM or highly OTM

   1. Deep ITM options already have high intrinsic value. Their time value is smaller and small changes in volatility have a smaller impact on price movements.

   2. Deep OTM options have a very low probability of expiring ITM, so small changes in implied volatility don’t move the needle much.

Ok, so the closer the option is to ATM, the higher the vega while the further away, the lower the vega. This makes the bond position (short a put spread) very interesting! Unlike the delta of the position, the vega of the position can theoretically “flip” from negative to positive as the bond declines in value. The vega of both put options are shown below (Figure 13). I’ve also included the combined vega of the position (Figure 14).

Figure 13: Vega of Both Put Options the Unsecured Bond Holder “Owns”

Figure 14: Vega of the Overall Unsecured Bond Position

This is extremely interesting (to me)! Past a certain point, the long bond position actually moves from short vol to long vol. While investment grade credit investors are undoubtedly short vol (right hand side of the graph), distressed debt investors are often long vol (left hand side of the graph). First, it may be helpful to justify this more explicitly.

1. When the EV is sufficiently low (~$100), the bought put struck at $100 is ATM meaning the vega is both long and maximized. The sold put is OTM and the vega is negative and small. Thus, the sum of these two is positive!

2. When the EV is higher, the sold put is always closer to ATM than the bought put, meaning bond investors are short vol throughout this “high EV” zone. 

The implications are profound. Rather than trying to minimize volatility of the EV, distressed credit investors should seek to maximize volatility as they are long vega. They should pursue turnaround strategies that seek to maximize uncertainty. The distressed debt investor has a positive delta and a positive vega, very similar to a call option on the underlying! Thus, for certain sections of EV, distressed creditors’ forecasts—and goals—should almost match that of the owner of a call option on the EV (Figure 15).

Figure 15: Distressed Creditors Resemble Owners of Long Call Options on EV

Conclusion

In this piece I have hopefully expanded on the idea that credit can be modeled using options theory. Rather than simply being short a put option on EV, unsecured creditors are, in effect, short one put option and long another. They are far more similar to sellers of put spreads than sellers of puts. Here are some key takeaways from this result.

1. Bondholders are always long delta—they want the value of the company to appreciate.

2. Bondholders are significantly more sensitive to the underlying value of the company when the company is insolvent than when it is doing particularly well.

   1. Perhaps distressed investors need to have more of a value-focus than IG (investment-grade) creditors. Small improvements in EBITDA have the potential to significantly change the value of distressed debt while only marginally effecting the value of IG bonds.

3. When a company is insolvent, creditors have a greater sensitivity to the underlying value of the company than equity owners.

4. Performing bonds are always short volatility—greater uncertainty in the value of the assets is negative for the credit.

5. Distressed creditors are often long volatility—greater uncertainty in the value of the company is often a positive for credit when the company is sufficiently insolvent.

6. Distressed creditors payoffs often mirror those of long call option traders—they hope for appreciation in asset value and higher volatility.

Thank You!

Thank you for reading until the end. Feel free to reach out if you have any questions or ideas on potential distressed scenarios to apply this framework to (either sovereign or corporate).

1. This ideas were greatly influenced by Michael Pettis and the Volatility Machine.